一、前言

这是在七夕写的一篇文章，在desmos的2d计算器上做了一个3d效果的跳动心形函数。这个函数是来源于shadertoy创始人之一的iq大佬（Inigo Quilez），使用的是一种称之为Signed Distance Functions（SDF，有符号距离函数）的方法。我将这个函数改为desmos 3d计算器上可以显示的版本，并且在这个基础上修改为2d版本，进行了动画的调整和着色

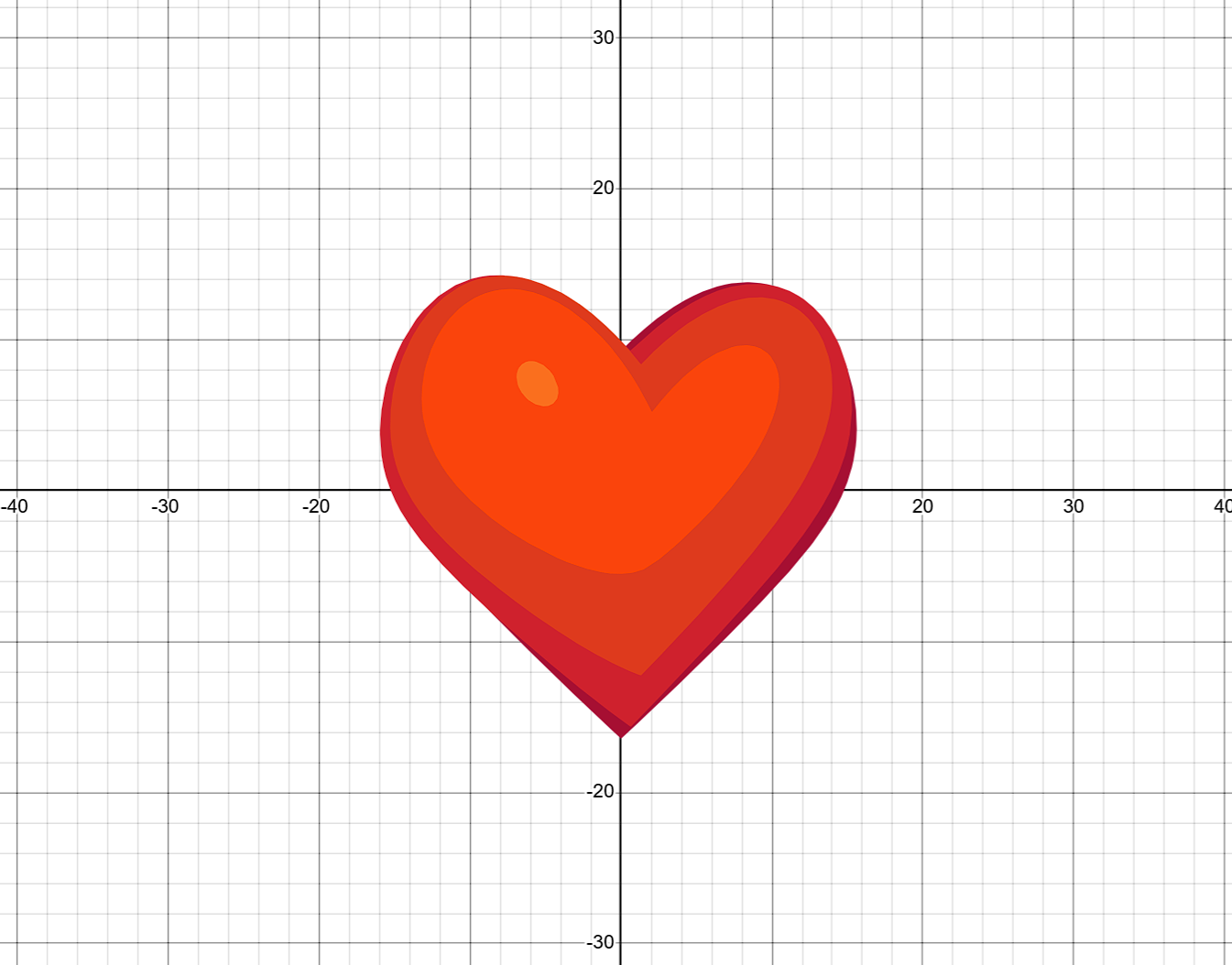
二、构造Signed Distance Functions（SDF，有符号距离函数）

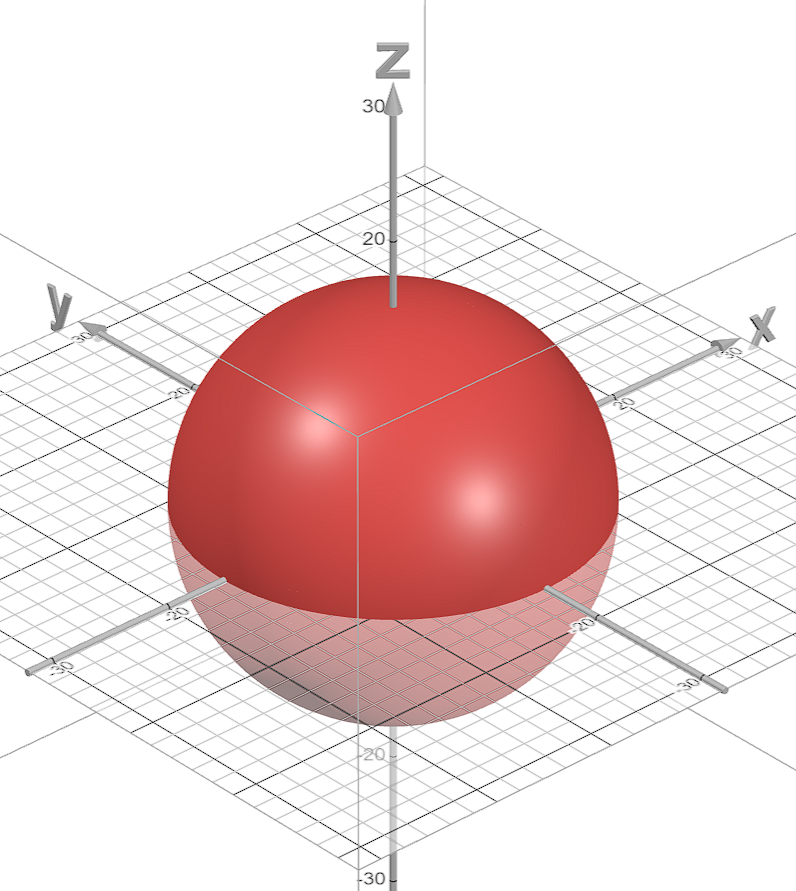
2.1 球体SDF

首先要构造一个球体函数，公式为：

S(x,y,z)=x2+y2+z2S\left(x,y,z\right)=x^{2}+y^{2}+z^{2}

当输入S(x,y,z)<152S\left(x,y,z\right)<15^{2}时可以得到一个半径为15的球体

2.2 调整y轴，得到半颗心

将y调整为一个斜着的抛物面的函数：

Y(x,y)=y−x(20−x40)Y\left(x,y\right)=y-x\left(\frac{20-x}{40}\right)

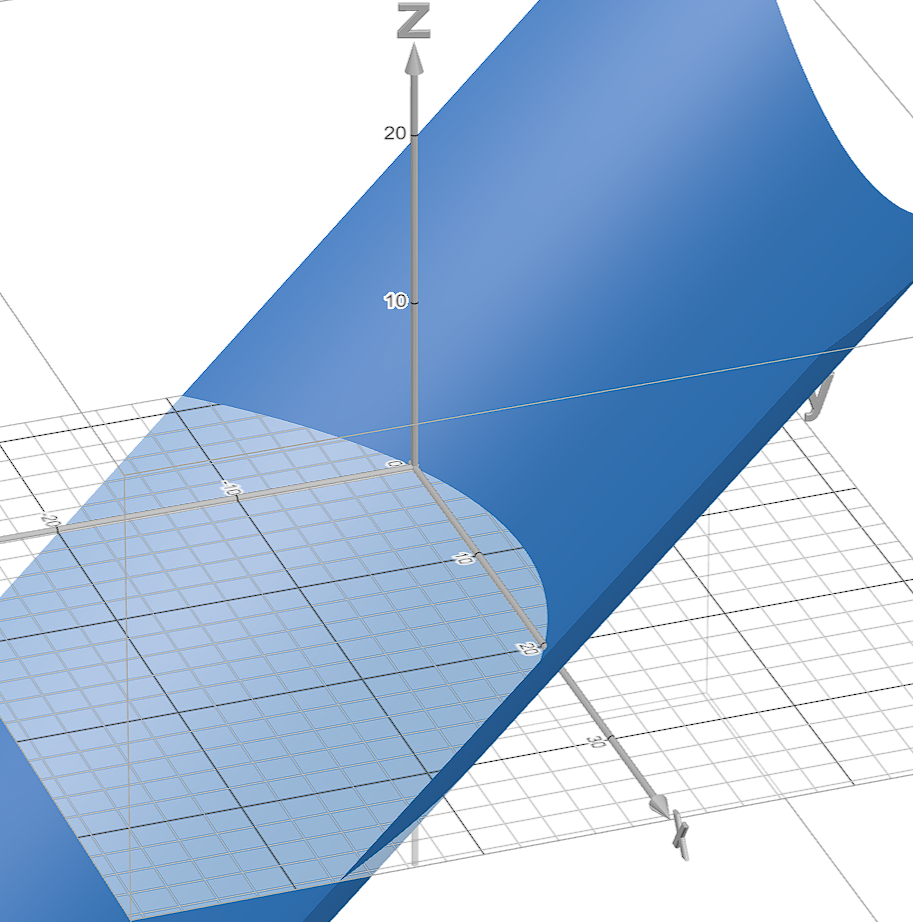
然后应用到球体函数中进行y的空间扭曲，得到半颗心的形状：

S(x,Y(x,y),z)=x2+y2+z2S\left(x,Y(x,y),z\right)=x^{2}+y^{2}+z^{2}

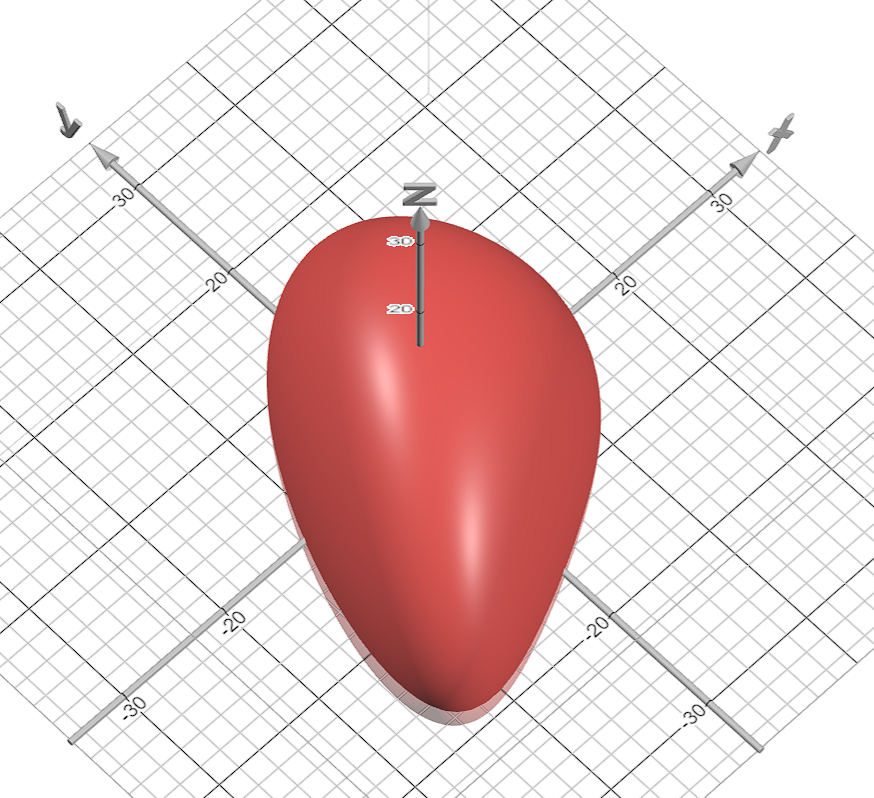
2.3 y轴对称并微调，得到对称的心

将y轴改为一个对称函数，做法就是加一个绝对值：

Y(x,y)=y−∣x∣(20−∣x∣40)Y\left(x,y\right)=y-\left|x\right|\left(\frac{20-\left|x\right|}{40}\right)

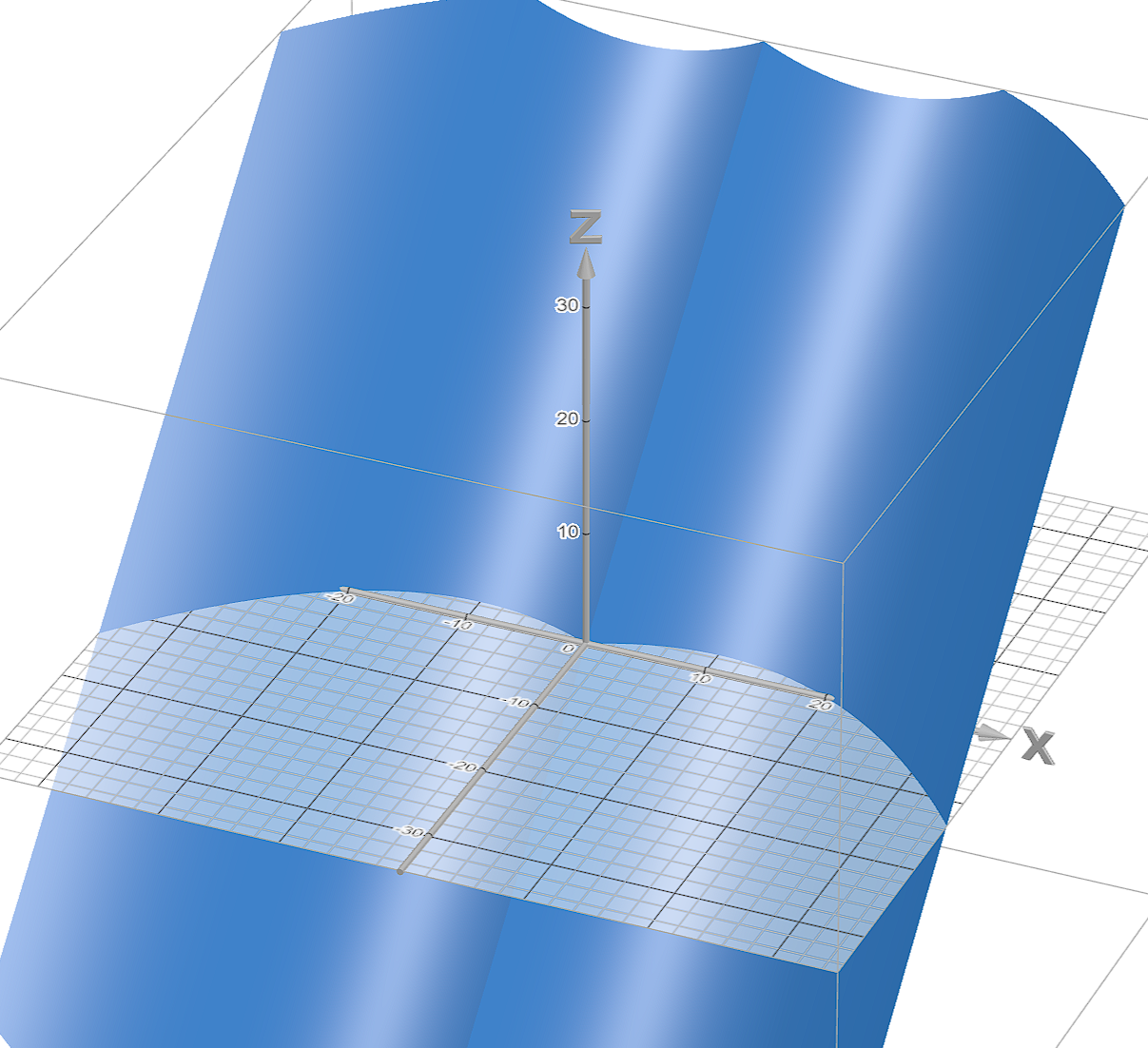
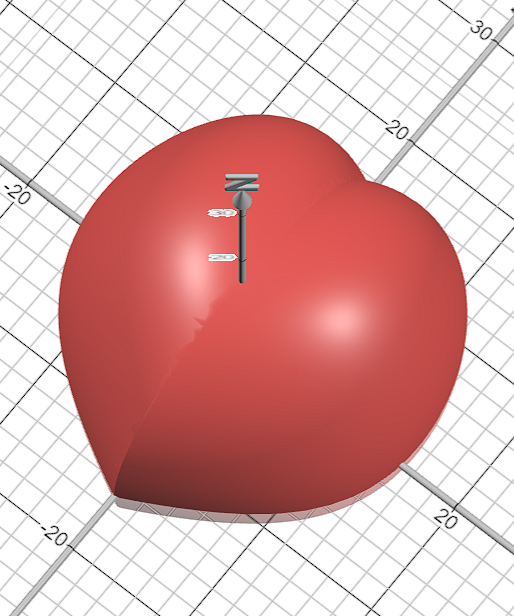
然后再对y轴函数微调，打磨一下心的形状：

Y(x,y)=4+1.2y−∣x∣20−∣x∣15Y\left(x,y\right)=4+1.2y-\left|x\right|\sqrt{\frac{20-\left|x\right|}{15}}

2.4 z轴调整心的厚度

从侧面看，心的厚度还需要进行调整

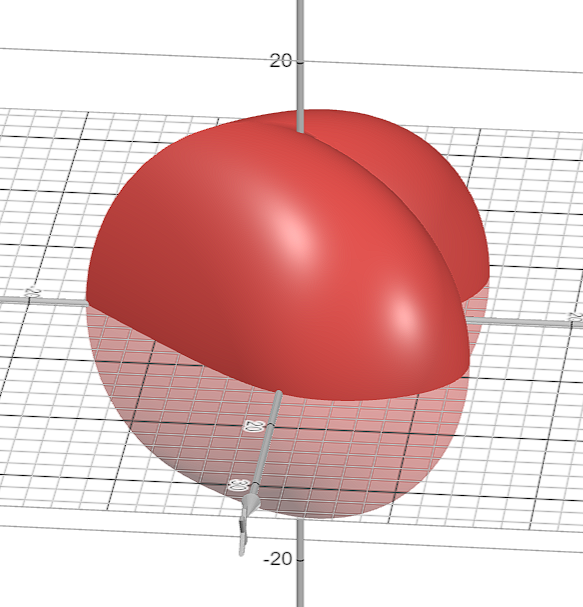
使用函数进行调整：

Z(y,z)=z(1.5−y25)S(x,Y(x,y),Z(y,z))<152Z\left(y,z\right)=z\left(1.5-\frac{y}{25}\right)\\ S\left(x,Y\left(x,y\right),Z\left(y,z\right)\right)<15^{2}

2.5 半径调整，做心跳动画

引入半径随时间变化的函数：

R(t)=15+3sin⁡(2πt)S(x,Y(x,y),Z(y,z))<R(t0)2R\left(t\right)=15+3\sin\left(2\pi t\right)\\ S\left(x,Y\left(x,y\right),Z\left(y,z\right)\right)<R\left(t_{0}\right)^{2}

其中t0t_0是一个不断增长的时间参数

在这个半径函数的基础上，做一些调整，让跳动更有生物感：

R(y,t)=15+3(12+12sin⁡(2πt+y25))4S(x,Y(x,y),Z(y,z))<R(y,t0)2R\left(y,t\right)=15+3\left(\frac{1}{2}+\frac{1}{2}\sin\left(2\pi t+\frac{y}{25}\right)\right)^{4}\\ S\left(x,Y\left(x,y\right),Z\left(y,z\right)\right)<R\left(y,t_{0}\right)^{2}

2.6 最终公式整理

S(x,y,z)=x2+y2+z2Y(x,y)=4+1.2y−∣x∣20−∣x∣15Z(y,z)=z(1.5−y25)R(y,r,t)=r+3(12+12sin⁡(2πt+y25))4H(x,y,z,r,t)=S(x,Y(x,y),Z(y,z))−R(y,r,t)2S\left(x,y,z\right)=x^{2}+y^{2}+z^{2}\\ Y\left(x,y\right)=4+1.2y-\left|x\right|\sqrt{\frac{20-\left|x\right|}{15}}\\ Z\left(y,z\right)=z\left(1.5-\frac{y}{25}\right)\\ R\left(y,r,t\right)=r+3\left(\frac{1}{2}+\frac{1}{2}\sin\left(2\pi t+\frac{y}{25}\right)\right)^{4}\\ H\left(x,y,z,r,t\right)=S\left(x,Y\left(x,y\right),Z\left(y,z\right)\right)-R\left(y,r,t\right)^{2}

其中rr为半径，提取出来方便调整，最终的效果的预览可以输入以下公式：

H(x,y,z,15,t0)<0H\left(x,y,z,15,t_{0}\right)<0

三、附加矩阵旋转

完成基础的SDF构造后，可以再加入一些整体的旋转，使用矩阵运算修改自变量x和z：

Hr(x,y,z,a,r,t)=H(xcos⁡a−zsin⁡a,y,xsin⁡a+zcos⁡a,r,t)H_{r}\left(x,y,z,a,r,t\right)=H\left(x\cos a-z\sin a,y,x\sin a+z\cos a,r,t\right)

其中aa为旋转角度，可以用以下公式预览结果：

Hr(x,y,z,t0,15,t0)<0H_{r}\left(x,y,z,t_{0},15,t_{0}\right)<0

四、3D转2D

4.1 不同高度轮廓截取

为了将3D转为2D，我们可以对3D模型的不同高度的轮廓截取下来，根据高度给不同颜色拼到2D上。我们可以简单地将自变量高度zz改为常数，例如获取高度0时的截面：

Hr(x,y,0,t0,15,t0)<0H_{r}\left(x,y,0,t_{0},15,t_{0}\right)<0

然后我们再将不同高度截面都获取到，并给不同的颜色，就可以得到基础的3D效果了（高度取 [0, 3, 6, …, 15]）：

4.2 动画微调，添加相机透视

我设计了一个转2D的函数方便调用：

H2d(x,y,z)=Hr((1−zs0)x,(1−zs0)(y+r04sin⁡πt0),z,4sin⁡πt08,r0,t0)H_{2d}\left(x,y,z\right)=H_{r}\left(\left(1-\frac{z}{s_{0}}\right)x,\left(1-\frac{z}{s_{0}}\right)\left(y+\frac{r_{0}}{4}\sin\pi t_{0}\right),z,4\sin\frac{\pi t_{0}}{8},r_{0},t_{0}\right)

其中：

  • r0r_0为半径常数，默认15，提取出来方便调整
  • s0s_0为相机透视参数，默认50

最终效果：

五、最后

最后借用iq大佬的一句话，“祝愿你们心中都有所爱”❤️