一、数学公式思路
数学公式链接:🔥FIRE🔥 | Desmos
对应的Shader实现链接:MathFireShader: 数学火焰Shader (gitee.com)
视频讲解:用数学公式绘制火焰特效!火焰渲染新思路探索_单机游戏热门视频 (bilibili.com)
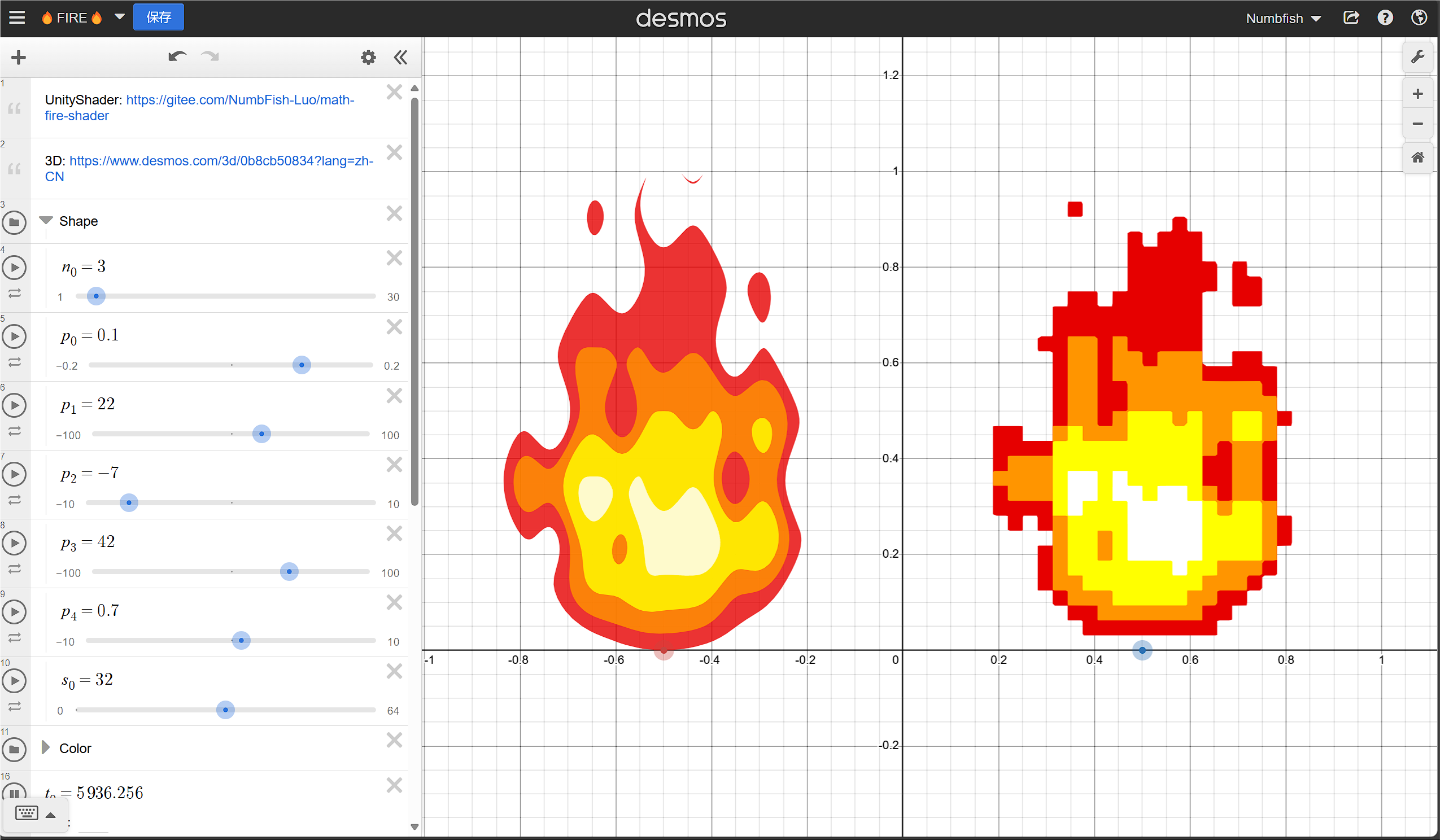
1.1 构造水滴形状
这个火焰特效的思路是,首先用一个水滴形状去绘制火焰的基本外轮廓。水滴函数为:
W(x,y)=(x2+y2)2−2y(x2+y2)+n0x2
其中的n0为一个常数,用于控制水滴的宽窄,默认用3。这个函数在3D中是一个这样的形状:
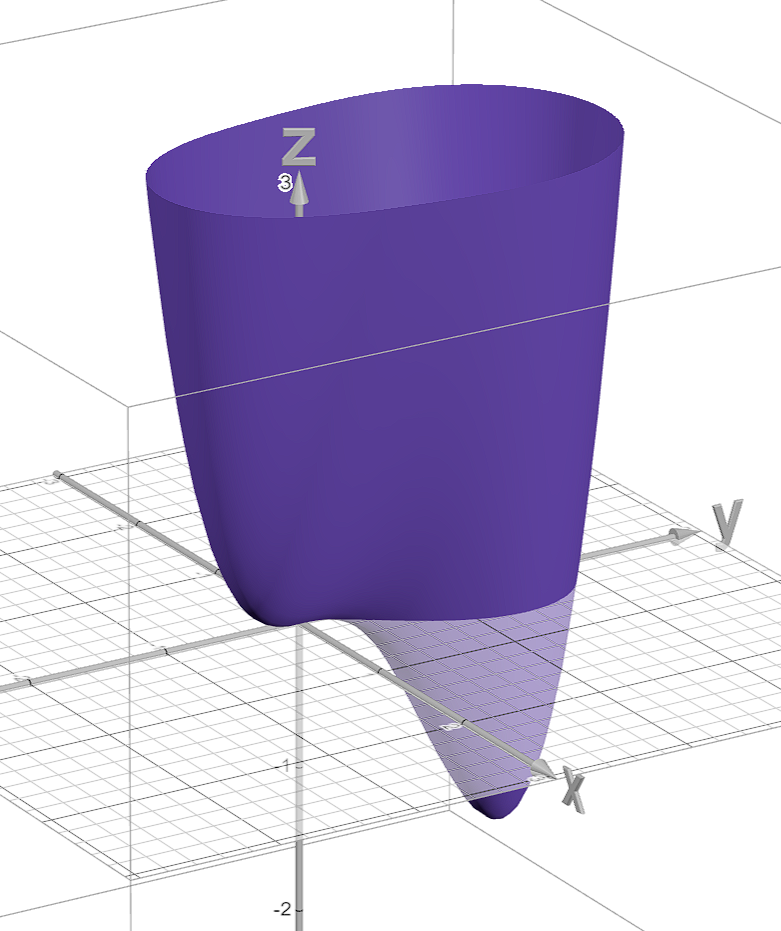
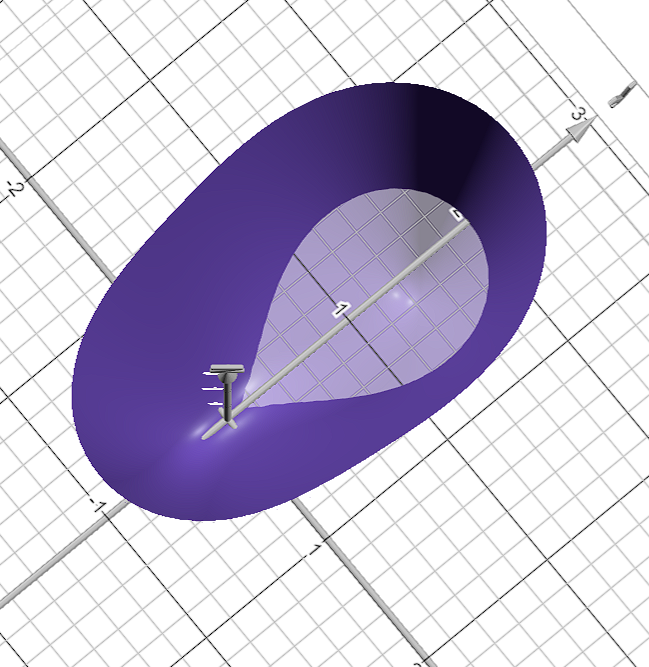
而在2D中则相当于截取了高度为0时的轮廓:
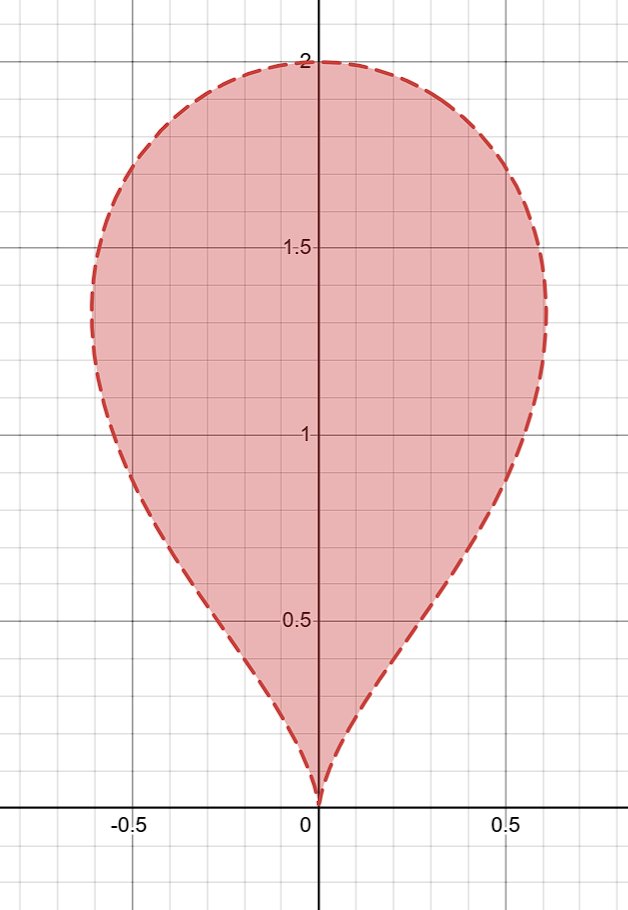
不过这个函数是倒过来的水滴,所以还需要微调一下,变成:
W0(x,y)=W(2x,2−2y)
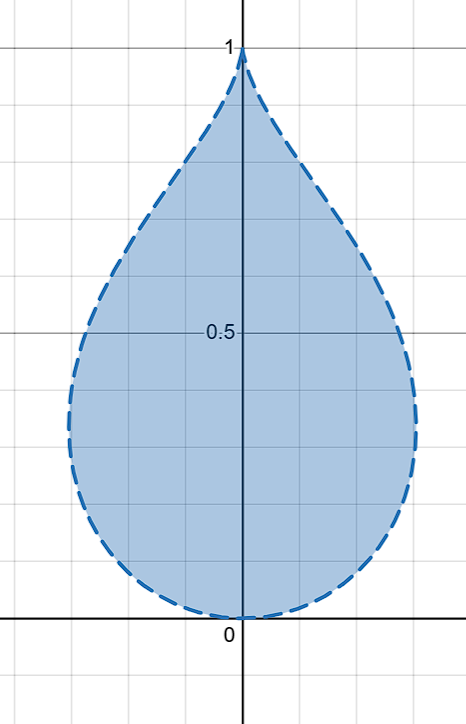
1.2 对水滴进行简易扭曲
扭曲水滴的方式,就是改变其自变量x和y,让它们随着时间发生变化即可,例如:
W0(x+10sin(10y+t0),y)<0
其中t0是一个不断变大的时间量,效果如下图:
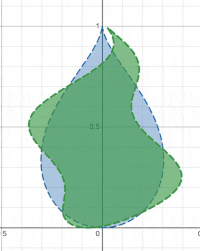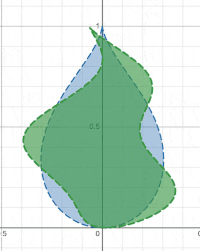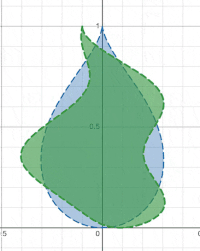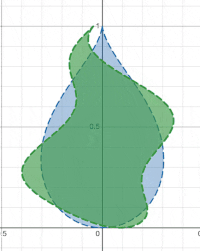
1.3 设计复杂扭曲
有了水滴扭曲的思路后,就可以开始制作一些更复杂的扭曲来模拟大火的随风飘动的破碎效果了,我设计的扭曲函数是:
O(x,y,t)=p0y(sin(p1y+p2t)+sin(p3x+p4t))
使用了三角函数去复杂化这个公式(用了类似于傅里叶级数的思想),其中的p0到p4都是这个扭曲函数的调整参数,默认值分别是0.1,22,-7,42,0.7。效果如下,是一堆从下往上冒出的气泡(下图是取了该函数大于0.1的区域):
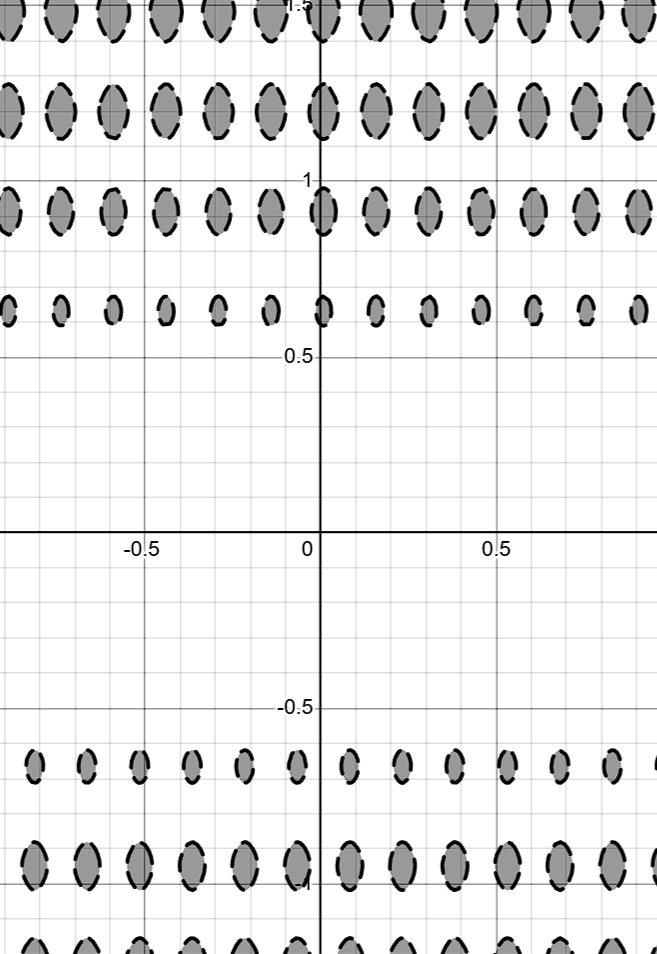
然后还需要对这些气泡进行限制,离火焰外轮廓太远的都要削弱气泡,削弱函数:
A(x,y)=max(0,1−W0(x,y))
将这两个函数相乘:
A(x,y)O(x,y,t)
得到的效果如下,是一个在水滴稍微往外一些的地方内冒泡的函数:
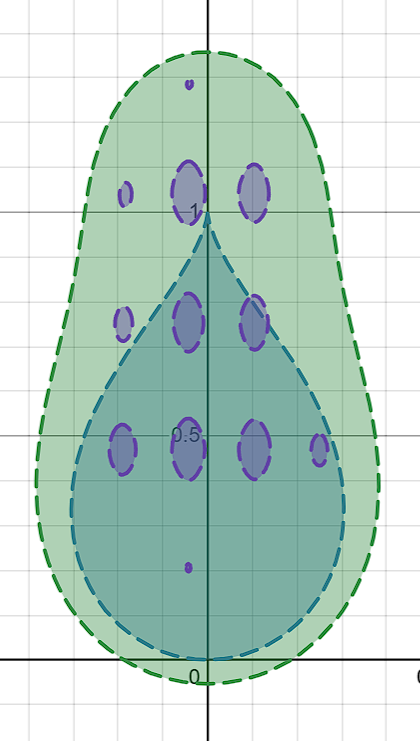
然后把这个扭曲函数应用到水滴函数中,得到最终公式:
F(x,y,t)=W0(x+A(x,y)O(x,y,t),y)
下面显示的是该函数小于0范围的轮廓:
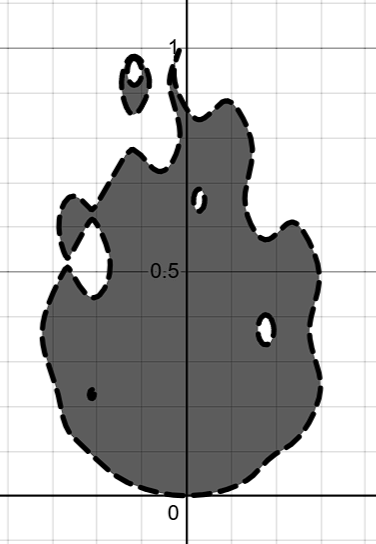
1.4 最终分层叠加
完成扭曲后,我们只需要把不同范围的轮廓叠加起来,并给不同的颜色,就能得到最终的效果了:

1.5 扩展:改为像素画风格
如果要改为像素画风格,我们需要把连续的自变量给离散化,将原本是0到1平滑变化的参数变成 [0.0, 0.25, 0.5, 0.75, 1] 这样的数组。我们设计像素化函数:
P(x,s)=sfloor(sx)
其中变量s决定了这个数组的增量是多少,如果填0.1就能得到 [0.0, 0.1, 0.2, …] 的数组,将其应用到函数F(x,y,t)中:
Fp(x,y,t)=F(P(x,s0),P(y,s0),t)
最终得到的结果就是像素画风格版本了:
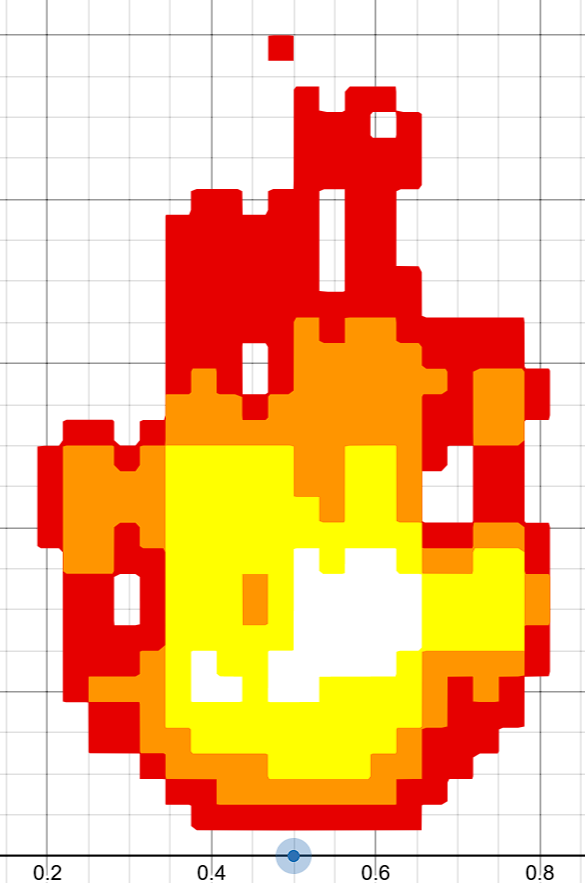
二、Shader实现
有了数学公式后,Shader实现很简单,我们还可以将函数F(x,y,t)的值直接输出成对应的颜色插值,在卡通风格,像素风格之外得到平滑渐变的基础风格。最终效果如下:

代码链接:MathFireShader: 数学火焰Shader (gitee.com)











